I’m Zelong LIU, a theoretical physicist at IHEP in Beijing. My research interests focus on perturbative quantum field theory and collider physics. My publication can be found in INSPIRE.

Research Interests

Standard Model Phenomenology

Precision tests of the Standard Model in particle physics is essential to understand the fundamental particles and their interaction comprehensively and accurately. Any deviation between experimental data and theoretical predictions could indicate the presence of new physics beyond the Standard Model.

The Large Hadron Collider (LHC) located at CERN near Geneva offers an excellent platform to explore the properties of elementary particles and forces at extremely high energies and tiny scales. The primary particles collided at the LHC are protons, consisting of quarks and gluons (also called partons). Quantum Chromodynamics (QCD) is a quantum field theory describing the strong forces, which govern the interactions between partons. Perturbative QCD is a powerful approach to obtain precise theoretical predictions for processes at hadron colliders. In practice, various observables receive sizable corrections from perturbative QCD, e.g. Higgs and top quark productions. Therefore, higher-order QCD calculations play a key role in explaining the experimental results and in revealing the properties of fundamental particles.

The computation of higher-order QCD corrections to a collider observable may entail a long journey, involving calculations of higher-loop scattering amplitudes and subtraction of infrared divergences in real emission.

Soft-collinear effective theory

Fixed-order results in perturbative QCD are not always reliable, in particular for the processes with a strong hierarchy of scales, because the large logarithms of ratio of scales violate the convergence of perturbative expansion in the strong coupling constant. To make a reliable theoretical prediction, we have to resum the large logarithms to all order in the strong coupling constant, and do expansion in the inverse of the logarithm.

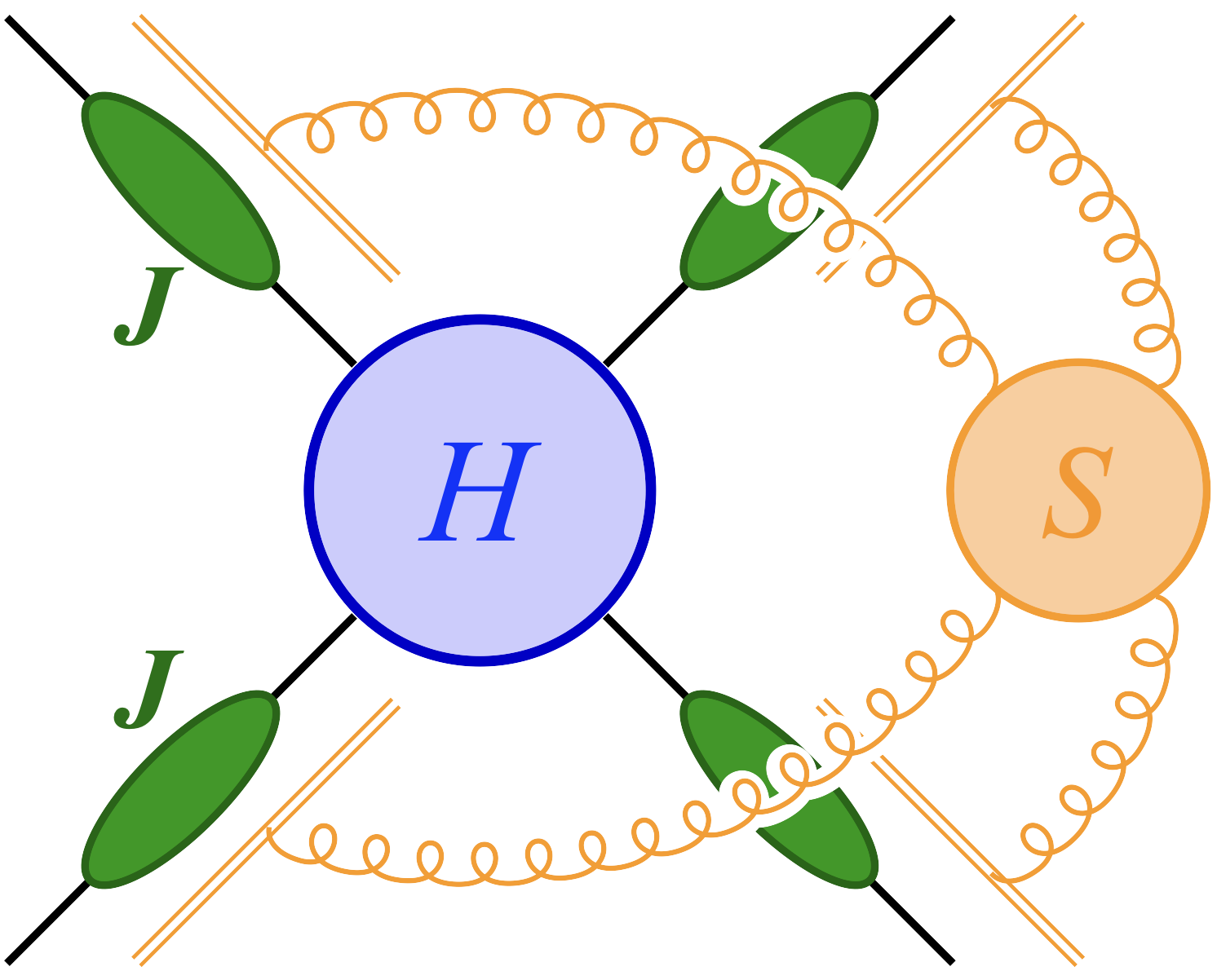
If an observable is sensitive to soft or collinear parton emissions, soft-collinear effective theory (SCET) provides a systematic way to separate the contributions from different momentum scales into a series of single scale problems. In other words, contributions from soft, collinear and hard interactions can be separated by factorization in SCET. The large logarithms can be resummed through the renormalization-group evolutions of Wilson coefficients or low-energy matrix elements between scales.

Factorization theorems in scale ratios have been established for many processes in the past decades. To improve the accuracy of resummation, it is crucial to investigate the infrared singularities of hard scattering amplitudes and to calculate higher-order corrections to low-energy matrix elements and Wilson coefficients.

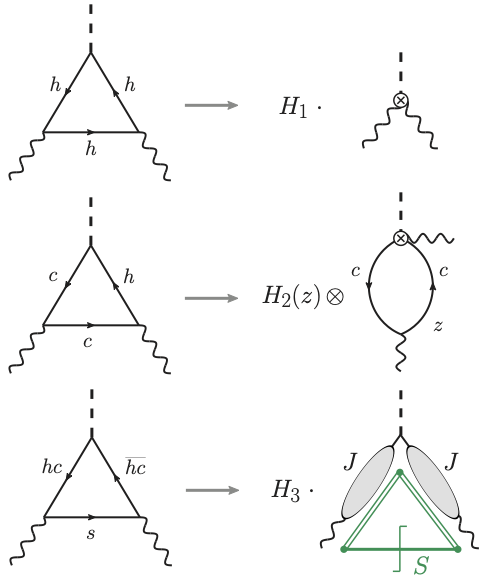
At leading power, a typical factorization theorem consists of a product of functions each associated with a single scale, while several complications arise at subleading power. It is still a big challenge to establish a rigorous factorization theorem due to the presence of endpoint divergences.